Aliasing
Wenn Du die Regel von mindestens zwei Samples pro Schwingungsperiode des Audiosignals missachtest, können unerwünschte Aliasing-Frequenzen erfasst werden. Aliasing steht für einen Identitätswechsel (wie bei James Bond / 007). Um das zu verhindern, muss vor dem Sampling ein "Anti-Alias"-Filter eingesetzt werden. Dies ist ein Low-Pass-Filter, der Frequenzen abschneidet, die über der halben Abtastrate liegen.
Diese Art Filter kann das Audiosignal beeinflussen. Oversampling (eine Überabtastung, bspw. durch Verdopplung oder Vervierfachung der Abtastfrequenz) wird verwendet, um den Einfluss des Filters zu reduzieren. (Eine Verdopplung der Abtastfrequenz bedeutet allerdings auch eine Verdopplung der entstehenden Daten für eine Aufnahme.)
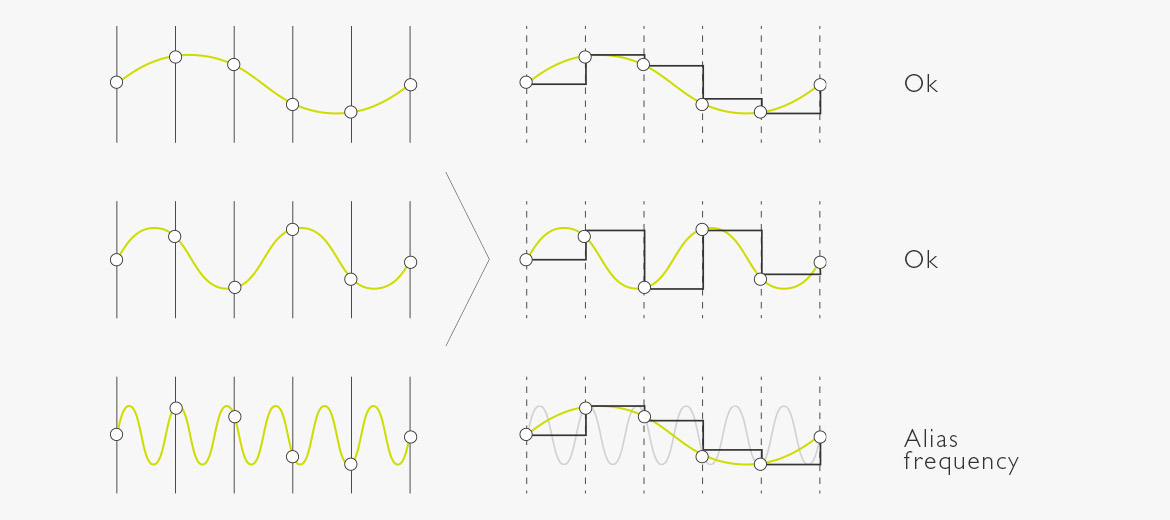 Abbildung 3. Abtastfrequenz
Abbildung 3. Abtastfrequenz
Wenn die Abtastfrequenz nicht mindestens dem Doppelten der höchsten Audiofrequenz entspricht, entspricht das rekonstruierte Signal nicht dem Eingangssignal.
Oben: Die eine Schwingung des Signals wird sechs Mal abgetastet / gesampelt. 6 > 2, also ist die Rekonstruktion okay.
Mitte: Die beiden Schwingungen des Signals werden sechs Mal abgetastet / gesampelt, was drei Abtastungen je Periode entspricht. 3 > 2, also ist die Rekonstruktion okay.
Unten: Die sechs Schwingungen des Signals werden sechs Mal abgetastet / gesampelt, was einer Abtastung je Schwingung entspricht. 1 < 2, also endet das Signal als Alias-Frequenz, die vom Original abweicht.
Jitter
Ein anderer sehr wichtiger Aspekt während einer Wandlung ist der Intervall zwischen den Samples. Jedes Intervall muss exakt die gleiche Länge haben, denn nach der Digitalisierung liegen keine Information über den Zeitpunkt eines Samples vor. Daher müssen wir uns auf eine stetige Wiederholung der Abtastung verlassen - ein konstantes Intervall. (Bei einer Samplingfrequeng von 48 kHz beträgt das Intervall zwischen zwei Samples 20.833 Mikrosekunden [µs].)
Der Abtast-Takt muss stabil sein und sollte durch nichts gestört werden. (Nicht-Exakte Abtastwiederholung, auch Jitter genannt, führt zu Rauschen im reproduzierten Audio-Signal.)
Quantisierung
Wie zuvor bemerkt, bildet jedes Sample eine Stelle im Original-Signal ab. Es ist wichtig, dass die Messung jedes Punkts und die gespeicherten Werte so genau wie möglich sind. Nach dem Abtastvorgang ist jede Referenz zum Originalsignal verloren.
Das Festlegen eines Werts zum Abtastzeitpunkt entspricht der Verwendung eines Maßbands in einer Werkstatt. Wenn Du einen Regalboden für Deinen Schrank aussägen möchtest, musst Du ihn ausmessen um zu ermitteln, wie groß er sein muss. Wenn Dein Maßband jetzt nur Meter oder Yards anzeigt, ist es nahezu unmöglich, die richtige Größe zu ermitteln. Wenn das Maßband auch Zentimeter oder Zoll anzeigt, wird die Genauigkeit schon besser. Der Boden mag aber immer noch nicht genau in den Schrank passen. Wenn das Maßband auch Millimeter oder Anteile von Zoll anzeigt, ist die Genauigkeit hoch genug, um die Größe zu beschreiben.
Der Begriff Quantisierung kommt vom lateinischen Wort 'quantitas', was Menge oder Größe bedeutet. Um die Größe eines Samples zu beschreiben, verwenden wir Bit. 'Bit' ist eine Zusammensetzung aus den Worten '
binary digi
t' (Binärziffer). Binär (Binary) bedeutet, die Ziffer kann nur einen von zwei Werten haben, 0 oder 1. Wenn wir größere Zahlen abbilden möchten, müssen wir mehr Bits verwenden. Beispielsweise erlaubt uns die Verwendung von zwei Ziffern die Abbildung von vier Werten: 00, 01, 10 und 11. Durch Hinzufügen weiterer Bits wird der Wertebereich durch jedes weitere Bit verdoppelt.
Die Genauigkeit der Messung - oder Quantisierung - wird durch die Menge an verfügbaren Bits für jedes Sample festgelegt. Jeder Bitwert repräsentiert einen vordefinierten Wert. Wenn der Originalwert genau einem der vordefinierten Werte entspricht, ist alles in Ordnung. Wenn dies nicht der Fall ist, musst Du den bestpassenden Wert hinnehmen. Das bringt allerdings einen Fehler mit sich, der nicht wieder kompensiert werden kann. Um also Fehler zu reduzieren ist es wichtig, eine hinreichende Zahl an Bits pro Sample zur Verfügung zu stellen. Wenige Bits pro Sample verursachen Verzerrung. Eine Erhöhung der Bits ändert die wahrgenommene Verzerrung in ein Rauschen. Dann bleibt die Frage, wie rauscharm Deine Wandlung sein soll. Generell verbessert sich das S/N-Verhältnis um 6 dB für jedes zusätzliche Bit.
Computer organisieren Bits in Gruppen zu 8, die bevorzugte (praktische) Anzahl an Bits pro Sample ist also 8, 16, 24, etc. 8 Bit pro Sample ist zu gering für einen hochwertigen Klang. Ein 16-Bit-Sample entspricht Klang in CD-Qualität. Für die Produktion von qualitativ hochwertigem Ton werden 24-Bit-Samples genutzt.
 Abbildung 4. Quantisierung
Abbildung 4. Quantisierung
Mit der Quantisierung bestimmt die Zahl der Bits die Genauigkeit des gelesenen Werts. Jedes Mal, wenn ein weiteres Bit zur Verfügung steht, verdoppelt sich die Auflösung der Skala und die Messfehler werden halbiert. In der Praxis bedeutet dies, dass das S/N-Verhältnis sich für jedes zusätzliche Bit um etwa 6 dB verbessert.
D-A
Bei der Wandlung von digital nach analog besteht die Aufgabe darin, ein Signal zu generieren, das proportional zu den Bitwerten ist, die in den digitalen Informationen enthalten sind. Jedes Bit repräsentiert dabei einen Spannungswert. Das wichtigste Bit (MSB) wandelt sich in die größte Spannung, das nächst signifikante Bit in die Hälfte dessen und so weiter, bis hin zum wenigsten signifikanten Bit (LSB). Durch die Addition aller Spannungsstufen und durch Aufrechterhaltung der aufsummierten Spannung bis zur Aktivierung des nächsten Samples wird ein kontinuierlicher Spannungsverlauf erzeugt. Das Signal wird dann wieder über einen Low-Pass-Filter geglättet.
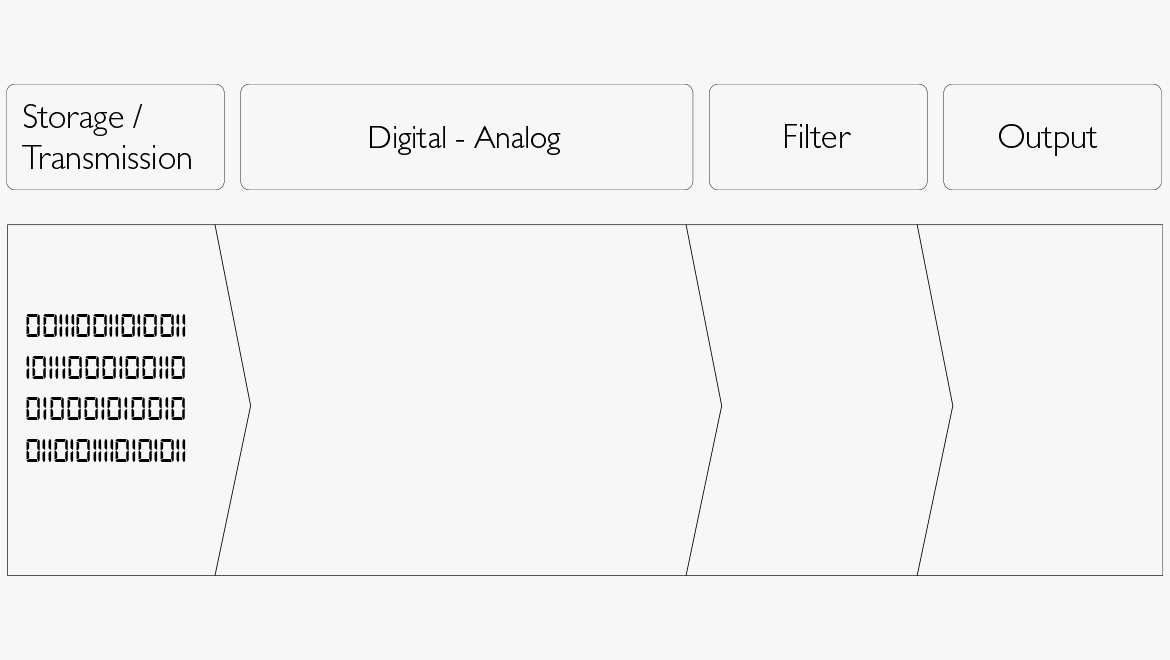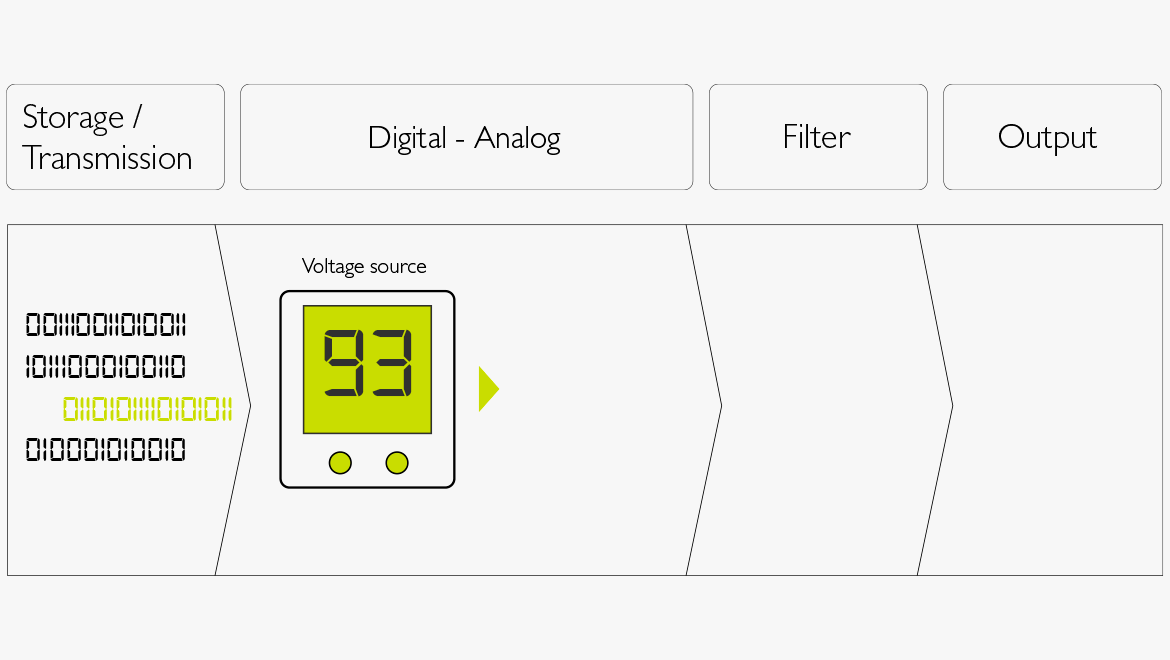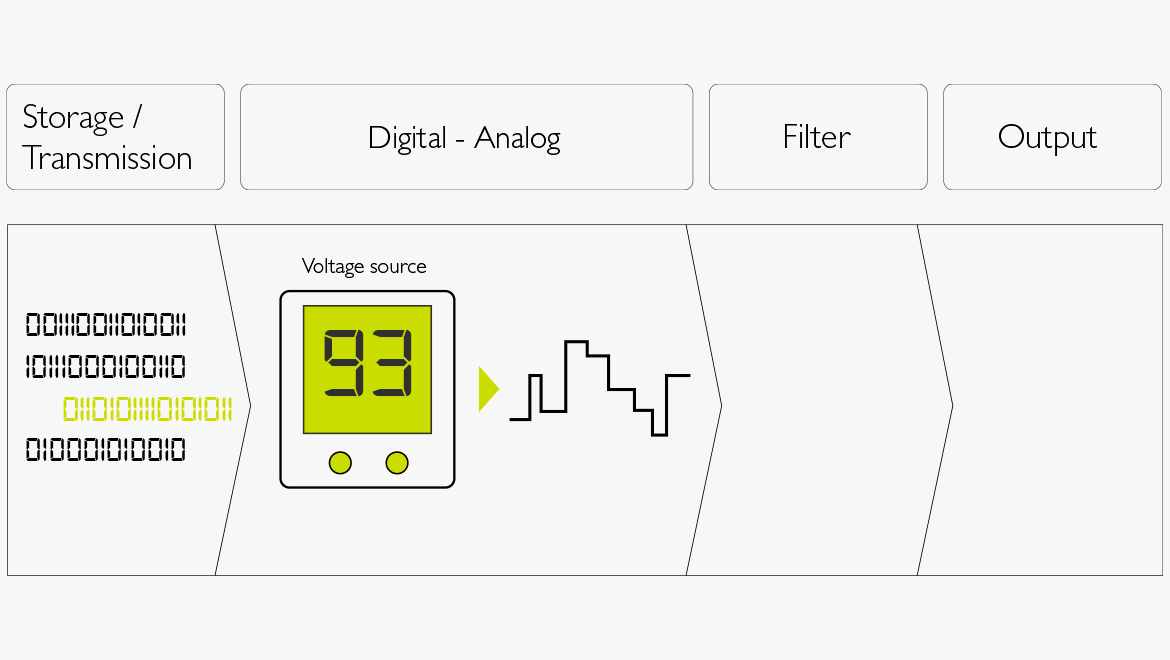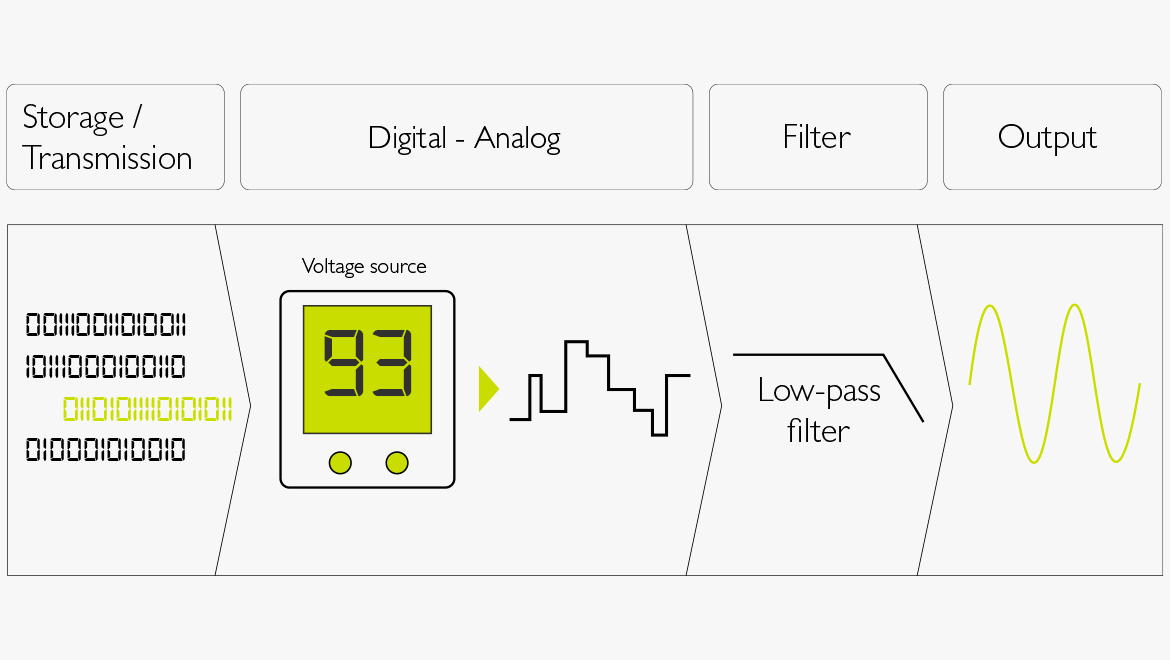 Abbildung 5. D/A-Wandlung
Abbildung 5. D/A-Wandlung
- Bei der Digital-Analog-Wandlung werden die gespeicherten Zahlen zurück in analoge Werte konvertiert.
- Die Zahlen werden in ein programmierbares Netzteil eingelesen, sodass sie entsprechende Spannungsstufen generieren können.
- Der Low-Pass-Filter glättet das Signal durch Entfernen der harmonischen Obertöne (die durch diese Stufen erzeugt werden), die oberhalb dieses Frequenzspektrums liegen.
- Der Ausgang ist rein analoges Audio.